Modulio ženklas, ko gero, yra vienas žinomiausių matematikos reiškinių. Tuo zv'yazku z tsim pas turtingus moksleivius po mitybos, kaip buduvat funkcijų tvarkaraščius, scho atkeršyti už modulį. Praneškime apie maisto grandinę.

1. Pobudova grafinės funkcijos, kuo pakeisti modulį

1 pavyzdys.

Indukuokite funkcijos y = x 2 - 8 | grafiką x | + 12.

Sprendimas.

Funkcijos paritetas yra reikšmingas. Y(-x) reikšmės yra paimtos iš y(x) reikšmių, todėl funkcija yra suporuota. Todi її tvarkaraštis simetriškas shdo osі Oy. Tai bus funkcijos y = x 2 - 8x + 12 grafikas, kai x ≥ 0, o Oy grafikas bus rodomas simetriškai neigiamam x (1 pav.).

užpakalis 2.

Būsimas tvarkaraštis mintis y = | x 2 - 8x + 12 |.

– Kokia yra siūlomos funkcijos apimtis? (y ≥ 0).

– Kaip perbraižytas grafikas? (Virš abscisės viršaus arba išsikišęs її).

Tse reiškia, kad funkcijos grafikas yra tokia tvarka: funkcijos y \u003d x 2 - 8x + 12 grafikas užpildys grafiko dalį, esančią virš linijos Ox, nesikeičiant, o grafiko dalis, esanti po abscisių linija, simetriškai rodo, kad ašiai Ox (2 pav.).

3 pavyzdys.

Norėdami paskatinti funkcijos y = | grafiką x 2 - 8 | x | + 12 | atlikti transformacijų derinį:

y = x 2 - 8x + 12 → y = x 2 - 8 | + 12 → y = | x 2 - 8 | x | + 12 |.

Pasiūlymas: 3 pav.

Pažvelkite į sąžiningos funkcijų transformaciją į visas funkcijas. Padarykime lentelę:

2. Pobudovos funkcijų grafikai, kaip formulėje "įterpti modulius"

Jau sužinojome apie kvadratinės funkcijos užpakalis, kaip atkeršyti modulį, taip pat apie pagrindines y = f (| x |), y = | formos funkcijų grafikų kūrimo taisykles. f(x) | ir y = |f(|x|)|. Qi transformacija padės mums valandą pažvelgti į įžeidžiantį užpakaliuką.

4 pavyzdys.

Pažiūrėkime į funkciją, kurios tipas y = |2 – |1 – |x|||. Viraz, kuris nustato funkciją, pašalinkite modulio įterpimą.

Sprendimas.

Pagreitinimas geometrinių transformacijų metodu.

Užsirašykime paskutinių pakeitimų ir zrobimo žibintus fotelio viduryje (4 pav.):

y=x → y=| x | → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1 | + 2 → y = | 2 - | 1 - | x | | |.

Pažiūrėkime į vipadki, jei simetrijos transformacija ir lygiagretus perkėlimas yra pagrindinė tvarkaraščių skatinimo technika.

5 pavyzdys.

Sukelkite funkcijos grafiką į formą y \u003d (x 2 - 4) / √ (x + 2) 2.

Sprendimas.

Pirmą kartą bus tvarkaraštis, perdarysime formulę, kuri yra duota funkcija, kuri atimama, kitu atveju funkcijos analitinė užduotis (5 pav.).

y = (x 2 - 4) / √ (x + 2) 2 = (x - 2) (x + 2) / | x + 2 |.

Rozkriёmo prie modulio reklamjuostės:

Jei x > -2, y = x - 2 ir x< -2, y = -(x – 2).

Paskirties sritis D(y) = (-∞; -2)ᴗ(-2; +∞).

Reikšmės sritis E(y) = (-4; +∞).

Taškai, kuriuose grafikas keičiasi išilgai koordinačių ašių: (0; -2) ir (2; 0).

Funkcija keičiasi per visus x intervalus (-∞; -2), auga iš x iš -2 iki +∞.

Čia turėjome galimybę iššifruoti modulio ženklą ir odos bėrimo funkcijos grafiką.

6 pavyzdys.

Pažiūrėkime į funkciją y = | x + 1 | - | x - 2 |.

Sprendimas.

Tyrinėjant modulio ženklą, būtina pažvelgti į skirtingus submodulio eilėraščių ženklų derinius.

Galbūt šiek tiek vipadki:

(x + 1 - x + 2 = 3, kai x ≥ -1 ir x ≥ 2;

(-x - 1 + x - 2 = -3, su x< -1 и x < 2;

(x + 1 + x - 2 = 2x - 1, jei x ≥ -1 i x< 2;

(-x - 1 - x + 2 = -2x + 1, su x< -1 и x ≥ 2 – пустое множество.

Ta pati išvaizdos funkcija matime look:

(3, jei x ≥ 2;

y = (-3, ties x< -1;

(2x – 1, kai -1 ≤ x< 2.

Mes pašalinome vienkartinio rinkinio funkciją, kurios grafikas pavaizduotas kaip mažas 6.

3. Funkcijų grafikų formavimo indukavimo algoritmas

y = a 1 | x - x 1 | + a 2 | x - x 2 | + … + a n | x - x n | + kirvis + b.

Prie priekinio užpakalio lengva atidaryti modulio ženklus. Jei modulių suma didesnė, tai problematiška žiūrėti į visas submodulių ženklų kombinacijas. Kaip galėčiau kam suplanuoti funkcijos tvarkaraštį?

Svarbu, kad grafas turi lamaną su viršūnėmis taškuose, kad abscisės gali būti -1 ir 2. Esant x = -1 ir x = 2 submoduliai lygūs nuliui. Praktiškai priartėjome prie taisyklės skatinti tokius tvarkaraščius:

Funkcijos grafikas forma y = a 1 | x - x 1 | + a 2 | x - x 2 | + … + a n | x - x n | + kirvis + b є laman su neišsenkamais ekstremaliais lankais. Norint sukelti tokį lamaną, pakanka žinoti visas її viršūnes (viršūnių abscisis є nulis pіdmodulnyh virazіv) ir vieną valdymo tašką kairėje ir dešinėje nenuluptų lankų.

Vadovas.

Indukuokite funkcijos y = | grafiką x | + | x - 1 | + | x + 1 | o žinoti yra mažiausiai svarbu.

Sprendimas:

Nulis submodulinių virusų: 0; -1; 1. Lamanoi viršūnės (0; 2); (-13); (13). Kontrolinis taškas dešiniarankis (2; 6), blogis (-2; 6). Bus tvarkaraštis (7 pav.). min f(x) = 2.

Pritrūko maisto? Nežinote, kaip suplanuoti funkciją su moduliu?
Norėdami gauti dėstytojo pagalbą – užsiregistruokite.

svetainėje, su visa arba privačia medžiagos kopija, išsiųsta į originalų obov'yazkove.

Modulis yra viena iš tų tylių kalbų apie visas čiulves, bet tiesą sakant, niekas paprastai nesupranta. Iki šios dienos bus puiki pamoka, užduotys į viršų iš modulių.

Iš karto pasakysiu: pamoka bus nepatogi. І vzagalі moduliai vzagalі tema yra ypač gremėzdiška. „Taigi, aišku, nepatogu! Mano smegenys auga! - Sakyčiau, daug mokosi, bet visos smegenys ištiriamos per tuos, kurių dauguma žmonių neturi žinių, bet kaip šūdas. Pirma pamoka – mėšlą paversti žiniomis.

Trochijos teorija

Taigi eime. Pradėkime nuo svarbiausio dalyko: kas yra modulis? Spėju, kad skaičiaus modulis yra toks pat skaičius, bet imk jį be minuso ženklo. Tobto, pavyzdžiui, $ \ left | -5 \dešinė | = 5 USD. Abo $\left | -129,5\dešinė | = 129,5 USD.

Ar viskas paprasta? Taip, paprasta. Ir kodėl vertas teigiamo skaičiaus modulis? Čia dar paprasčiau: teigiamo skaičiaus modulis lygus pačiam skaičiui: $ \ left | 5\dešinė | = 5 USD; $\left| 129,5\dešinė | = 129,5 USD ir tt

Išeiti iš tsіkava rіch: skirtingi skaičiai gali būti tas pats modulis. Pavyzdžiui: $ \ left | -5 \right|=\left| 5\dešinė | = 5 USD; $\left| -129,5 \right|=\left| 129,5\dešinė | = 129,5 USD. Nesvarbu, ar kai kurių modulių skaičiai yra vienodi: skaičiai yra vienodi. Taip pat svarbu pažymėti, kad priešingų skaičių modulis yra lygus:

\[\left| -a \right|=\left| a\right|\]

Kitas svarbus faktas: modulis jokiu būdu nėra neigiamas. Jie paėmė skaičių mi - net jei jis yra teigiamas, jei jis yra neigiamas - jogo modulis visada bus teigiamas (arba kraštutiniu atveju jis bus nulis). Dėl šios priežasties modulis dažnai vadinamas absoliučia skaičiaus verte.

Be to, kadangi galima priskirti modulį teigiamam ir neigiamam skaičiui, tai visiems skaičiams būtina priskirti visuotinį modulį. Ir pats: skaičiaus modulis yra lygus pačiam skaičiui, jei skaičius yra teigiamas (arba nulis), arba jei skaičius lygus priešingam skaičiui, jei skaičius yra neigiamas. Galite užrašyti tą pačią formulę:

Daugiau yra nulio modulis, bet vin zavzhdi yra lygus nuliui. Be to, nulis yra vienas, nes nėra priešingybės.

Tokiu būdu pažvelkime į $ y = \ left | x \right|$ ir pabandykite nupiešti її tvarkaraštį, tada pamatysime šį „aušrą“:

Modulio ir tobulumo užpakalio grafikas

Paveikslėlio apačioje aiškiai matote, kad $ \ left | -m \right|=\left| m \right|$, o modulio grafikas nenusileidžia žemiau x ašies. Ir vis dėlto ne viskas: raudona linija žymi tiesę $y=a$, taigi su teigiamu $a$ duoda dvi šaknis: $((x)_(1))$ і $((x)_(2)) $, bet apie jas pakalbėkime vėliau. :)

Grynai algebrinio dizaino kremas yra labiau geometrinis. Gali būti, kad skaičių eilutėje yra du taškai: $((x)_(1))$ i $((x)_(2))$. І čia viraz $\left| ((x)_(1))-((x)_(2)) \right|$ – nejudėkite tik tarp nurodytų taškų. Abo, kaip visada, geras vіdrіzka, scho zadnuє tsі taškai:

Kurio pavadinimas taip pat tariamas, kad modulis visada yra neigiamas. Pereikime prie dešinės lygybės.

Pagrindinė formulė

Na, harazd, jie išėjo iš susitikimų. Ale nesijautė geriau. Kaip patikrinti lygį, ką reikėtų daryti su šiuo moduliu?

Ramiai, bet ramiai. Pradėkime nuo paprasčiausių kalbų. Pažvelkime į kažką panašaus:

\[\left| x\right|=3\]

Taigi, pridėkite $x$ 3 modulį. Prie ko galite pridėti $x$? Na, sprendžiant iš paskyrimo, mes esame visiškai valdžioje $x=3$. Diyno:

\[\left| 3\right|=3\]

Kokie kiti skaičiai? Cap nibi traukia, scho є. Pavyzdžiui, $ x = -3 $ - naujam $ \ left | -3 \dešinė | = 3 USD, tada. laimi būtina pusiausvyra.

Tada galbūt juokaudami pagalvokite, ar mes žinome skaičius? Ir ašis sulaužyta: nebėra skaičių. Rivnyannia $ \ liko | x \right|=3$ gali turėti tik dvi šaknis: $x=3$ ir $x=-3$.

Dabar trochus galima sutvarkyti. Tegul funkcija $f\left(x \right)$ pasikeičia po modulio ženklu, o dešiniarankis tripleto pakaitalas gali būti nustatytas pakankamu skaičiumi $a$. Mes priimame vienodus:

\[\left| f\left(x \right) \right|=a\]

Na, o kaip virišuoji? Spėliojimas: $f\left(x \right)$ yra gana funkcija, $a$ yra skaičius. Tobto. vzagali be-yak! Pavyzdžiui:

\[\left| 2x+1 \right|=5\]

\[\left| 10x-5 \right|=-65\]

Geriausia pagarba vienas kitam yra lygi. Apie naują akį galima pasakyti: naujoje nėra šaknų. Kodėl? Viskas teisinga: ko reikia naujame, kad modulis būtų pridėtas prie neigiamo skaičiaus, kurio mes niekada nežinome, mes jau žinome, kad modulis yra teigiamas skaičius arba nulis kraštutiniu atveju.

O ašis nuo pirmųjų lygių smagiau. Čia yra dvi parinktys: arba po modulio ženklu būti teigiamas, o tada $ \ left | 2x+1 \right|=2x+1$, kitu atveju ce viraz vis tiek neigiamas, taigi $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$. Iš pirmo žvilgsnio mūsų lygus bus perrašytas taip:

\[\left| 2x+1 \right|=5\rodyklė dešinėn 2x+1=5\]

Ir nesunku suprasti, kad submodulinė virazė $2x+1$ yra veiksmingai teigiama – iki skaičiaus 5. Štai ir viskas. galime ramiai virishuvati tse rivnyannia - atimti šaknis bus shmatkom vіdpovіdі:

Ypatingai nepasitikintys, jie gali pabandyti įdėti žinias apie kitos lygties pusės šaknis ir jas pakeisti, o tai bus teigiamas skaičius teisingame modulyje.

Dabar pažvelkime į neigiamą submodulinę virusazę:

'

Oi! Viską aiškiai žinau: leidome tą $2x+1 \lt 0$, ir dėl to atėmėme tą $2x+1=-5$ — ce viraz mažiau už nulį. Virishuemo otrimane equal, su kuriuo jau tikrai žinote, kad žinios yra mūsų šaknis:

Tuo pačiu metu mes vėl atėmėme du grąžinimus: $ x = 2 $ і $ x = 3 $. Taigi, bendra kaina buvo tris kartus didesnė, mažesnė nei paprastas lygias $\left| x \right|=3$, bet niekas nepasikeitė. Tada galbūt yra universalus algoritmas?

Taigi, toks algoritmas yra žinomas. І iš karto mi yogo razberemo.

Zvіlnennya pagal modulio ženklą

Duokime mums lygų $ \ left | f\left(x \right) \right|=a$ ir $a\ge 0$ (dabar, kaip jau žinome, šaknies nėra). Tada galite praleisti modulio ženklą už šios taisyklės:

\[\left| f\left(x \right) \right|=a\Rightarrow f\left(x \right)=\pm a\]

Šiame reitinge mūsų suderinimas su moduliu skyla į du, bet net ir be modulio. Ašis ir visa plėtra! Pabandykime virishiti kіlka rivnyan. Išimkime ašį iš to

\[\left| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]

Okremo razglyanaem, jei dešinė yra tuzinas su pliusu, o okremo jei su minusu. Maemo:

\[\begin(align)& 5x+4=10\Rightarrow 5x=6\Rightarrow x=\frac(6)(5)=1,2; \\& 5x+4=-10\Rightarrow 5x=-14\Rightarrow x=-\frac(14)(5)=-2.8. \\pabaiga (lygiuoti)\]

Nuo aš visų! Jie laimėjo dvi šaknis: $ x = 1,2 $ ir $ x = -2,8 $. Visi sprendimai užėmė tiesiog dvi eilutes.

Gerai, jokio maisto, pažiūrėkime šiek tiek rimčiau:

\[\left| 7–5x \right|=13\]

Iš naujo atidarau modulį su pliusu ir minusu:

\[\begin(align)& 7-5x=13\Rightarrow -5x=6\Rightarrow x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\RightArrow -5x=-20\Rightarrow x=4. \\pabaiga (lygiuoti)\]

Pradedu kelias eilutes – ir aš pasiruošęs! Kaip sakiau, moduliuose nėra nieko sulankstomo. Geriau atsiminti šprotų taisykles. Tam mes davėme ir tęsėme tinkamas lankstymo užduotis.

Vipadok zminnoy dešinioji dalis

O dabar pažvelkime į šį išlyginimą:

\[\left| 3x-2 \right|=2x\]

Tse lygus iš principo vіdrіznyaєtsya vіd pperednіh. Čimas? O mes, dešiniarankiai $2x$ kaštų ekvivalentiškumo ženkle – ilgai negalime žinoti, kas yra teigiama, o kuri neigiama.

Kaip tau šis laikas? Pirmiausia reikia kartą ir visiems laikams suprasti, ką jei lygybės dalies teisės atrodo neigiamos, tai lygybė nėra šaknis- jau žinome, kad modulis negali būti lygus neigiamam skaičiui.

Ir kitaip, jei dešinioji dalis vis dar yra teigiama (kitaip ji lygi nuliui), galite dirbti taip pat, kaip ir anksčiau: tiesiog išplėsti modulį pliuso ir minuso ženklu.

Tokiu būdu suformuluojame taisyklę papildomoms funkcijoms $f\left(x \right)$ ir $g\left(x \right)$ :

\[\left| f\left(x \right) \right|=g\left(x \right)\Rightarrow \left\( \begin (lygiuoti)& f\left(x \right)=\pm g\left(x \right) ), \\& g\left(x \right)\ge right 0. \\\end.

Mes pašaliname pavydą:

\[\left| 3x-2 \right|=2x\RightArrow \left\( \begin (lygiuoti)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(lygiuoti) \right.\]

Na, gal $2x\ge 0$, atrodo, ilsimės. Tiesą sakant, galite kvailai įsivaizduoti šaknį, kaip atimame iš pirmo lygio, ir apverčiame: kuo skiriasi chi ir ne.

Prie to mes atsiesime patį pavydą:

\[\begin(align)& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\RightArrow 3x=0\RightArrow x=0. \\pabaiga (lygiuoti)\]

Na, yak z tsikh dvoh korenіv tenkina gal $2x\ge 0$? Taigi abu! Štai kodėl jūs turite du skaičius: $ x = (4) / (3) \; $ i $ x = 0 $. Ašis ir visi sprendimai.

Įtariu, kad kai kurie mokiniai jau pradėjo blogai jaustis? Na, pažvelkime į daugiau lankstymo:

\[\left| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\]

Net jei tai atrodo kenkėjiška, iš tikrųjų visi jie prilygsta „gerų funkcijų modulio“ tipui:

\[\left| f\left(x \right) \right|=g\left(x \right)\]

O pasirodo kaip tik taip:

\[\left| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\Rodyklė dešinėn \kairė\( \begin(lygiuoti)& ( (x)^(3))-3(x)^(2))+x=\pm \left(x-((x)\(3) \^(3) \^(3) \ ^(3) . \\\pabaiga (lygiuoti) \dešinė.\]

Iš mano nervingumo tada išsiaiškinsime – tai lyg ir turėtų būti blogis (tai tikrai paprasta, bet jogos nepažeisime). Kol kas pasirūpinkime otrimanimy lygiais. Matome pirmąjį kritimą – jei modulis atidaromas su pliuso ženklu:

\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]

Na, čia supratau, kad reikia, kad visi broliai būtų blogi, atsivestų panašius ir stebėtųsi tuo, ką matome. Ir pažiūrėkite į ašį:

\[\begin(lygiuoti)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\pabaiga (lygiuoti)\]

Dėl pančių kaltinkite didelį daugiklį $((x)^(2))$ ir paimkite dar paprastesnį lygumą:

'

\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1,5.\]

Čia buvome pagerbti svarbia kūrybos galia, dėl kurios turtingą terminą suskirstėme į kartotinius: tvir lygus nuliui, jei norite, kad vienas iš daugiklių lygus nuliui.

Dabar mes patys su kitais lygiais išsiaiškinsime, ką įvesti atidarant modulį su „minuso“ ženklu:

\[\begin(lygiuoti)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\left(-3x+2 \right)=0. \\pabaiga (lygiuoti)\]

Žinau tą patį: tvir lygus nuliui, jei lygus nuliui, noriu vieno iš kartotinių. Maemo:

\[\left[ \begin (lygiuoti)& x=0 \\& -3x+2=0 \\\end (lygiuoti) \right.\]

Na, iš mi buvo atimtos trys šaknys: $ x = 0 $, $ x = 1,5 $ i $ x = (2) / (3) \; Na, o kaip su pide rinkiniu vіdpovіd? Kam, atspėkime, ką galime padaryti, matydami nelygumus:

Kaip vrahuvati tsiu vimogu? Taip lengva įsivaizduoti, kad šaknis randama ir ją galima pakartotinai patikrinti: tsikh $x$ chi ni atveju yra skirtumas. Maemo:

\[\begin(align)& x=0\Rodyklė dešinėn x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Rodyklė dešinėn x-((x)^(3))=1,5-((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Rodyklė dešinėn x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27) ge 0; \\pabaiga (lygiuoti)\]

Šiame reitinge šaknis $ x = 1,5 $ mums nepriklauso. Turiu tik dvi šaknis:

\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]

Kaip bachitas, galvoje neturėjau nieko nuoseklaus - modulių išlyginimas visada priklauso nuo algoritmo. Būtina geriau mokytis apie turtingus narius ir neatitikimus. Pereikime prie lankstymo užduočių – jau bus ne vienas, o du moduliai.

Lygiavimas su dviem moduliais

Dosі mi vyvchali mažiau nei paprasčiausias rіvnyannya - yra tik vienas modulis ir daugiau. Ištaisėme "kaip tik dabar" į kitą nelygumo dalį, įdėjome modulį, kad rezultatas būtų lygus $ \ liko | f\left(x \right) \right|=g\left(x \right)$ arba pereikite prie paprasto $\left| f\left(x \right) \right|=a$.

Ale, vaikiškas sodas baigėsi – atėjo valanda pažvelgti rimčiau. Pažvelkime į šį tipą:

\[\left| f\left(x \right) \right|=\left| g\left(x \right) \right|\]

Proto reikšmė „modulis yra toks pat kaip modulis“. Iš esmės svarbus momentas yra kitų papildymų ir kartotinių buvimas: tik vienas kairiarankis modulis, kitas dešiniarankis modulis - ir nieko daugiau.

Tiesiog pagalvokite iš karto, kad toks vienodas kintamumas yra blogesnis, sumažinkite tuos, kuriuos pasiekėme. Ir ašis i nі: tsі rivnyannya virіshuyusya navіt paprasčiau. Ašies formulė:

\[\left| f\left(x \right) \right|=\left| g\left(x \right) \right|\Rightarrow f\left(x \right)=\pm g\left(x \right)\]

Ūsai! Paprasčiausiai palyginame submodulinius virazi, prieš vieną iš jų padėdami pliuso arba minuso ženklą. Ir tada mes atimsime du lygius - ir šaknis yra paruošta! Kasdien dodatkovyh obmezhen, zhestnyh nerыvnosti tiesiog. Viskas paprasta.

Pabandykime šią užduotį:

\[\left| 2x+3 \right|=\left| 2x-7 \right|\]

Elementaru, Vatsonai! Atidaromi moduliai:

\[\left| 2x+3 \right|=\left| 2x-7 \right|\RightArrow 2x+3=\pm \left(2x-7 \right)\]

Pažvelkime į odos vapadoką:

\[\begin(align)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\left(2x-7 \right)\Rodyklė dešinėn 2x+3=-2x+7. \\pabaiga (lygiuoti)\]

Pirmasis lygus neturi šaknies. Kodėl, jei $ 3 = - 7 $? Kokioms $x$ vertėms? „Kas, po velnių, yra $x$? Ar tu užmėtytas akmenimis? Ten nėra daug $x$“, – sakote jūs. Aš būsiu teisus. Mes gavome lygiavertiškumą, kad negalėtume palikti nuošalyje keičiamų $x$ pavidalu, o pats lygiavertiškumas yra neteisingas. Štai kodėl nėra šaknies.

Su kitais lygiais visi trochai yra neaiškūs, bet ir vis paprasčiau:

Kaip ir Bachimo, viskas vyko pažodžiui poroje eilučių - kitos eilutės eilutės neskaičiavome.

Rezultatas turi likutinę vertę: $ x = $1.

Nu jakas? Svarbu? Akivaizdu, kad ne. Pabandykime dar kartą:

\[\left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\]

Žinau, kad mes lygūs protui $ \ left | f\left(x \right) \right|=\left| g\left(x \right) \right|$. Prie to iš karto perrašome jogą, atskleisdami modulio ženklą:

\[((x)^(2))-3x+2=\pm \left(x-1 \right)\]

Gali būti, kad kažkas iš karto klausia: „Ei, koks čia švyturys? Kodėl „pliusas-minusas“ yra dešinėje, o ne kairėje? Leiskite man akimirksniu viską paaiškinti. Gerąja prasme esame kalti perrašę savo lygius taip:

Tada reikės atverti arkas, visus papildymus perkelti į vieną bloką su lygybės ženklu (lygybės skeveldros, aišku, į abi puses bus kvadratinės), tą ir toli šaknį. Tačiau palaukite minutę: jei „pliusas-minusas“ stovi prieš tris dodankus (ypač jei vienas iš jų yra kvadratinis virazas), tai atrodo labiau sulankstoma, žemesnė situacija, jei „pliusas-minusas“ mažiau stovės prieš du dodankus.

Ir vis dėlto mums nėra svarbu perrašyti dieną taip:

\[\left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\Rightrow \left| ((x)^(2))-3x+2 \right|=\left| x-1 \right|\]

Kas nutiko? Tai nieko ypatingo: jie tiesiog prisiminė liūtą ir teisingą misijos dalį. Dribnitsa, kaip trochas, atleisk mums gyvenimą. :)

Akimirksniu tai lygu, žiūrint į parinktis su pliusu ir minusu:

\[\begin(lygiuoti)& ((x)^(2))-3x+2=x-1\Rodyklė dešinėn ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\left(x-1 \right)\Rodyklė dešinėn ((x)^(2))-2x+1=0. \\pabaiga (lygiuoti)\]

Pirmoji lygi šaknis yra $x=3$ ir $x=1$. Kitas vzagalі є tikslus kvadratas:

\[((x)^(2))-2x+1=((\left(x-1 \right))^(2))\]

Tam yra tik viena šaknis: $x=1$. Ale tse šaknys jau buvo nupjautos anksčiau. Tokia tvarka pіdsumkov vіdpovіd turės tik du skaičius:

\[((x)_(1))=3;\quad ((x)_(2))=1.\]

Ponia vikonan! Galite paimti pyragą iš policijos ir gauti. Yra 2, jūsų vidurkis.

Pagarba pagarba. Tos pačios šaknies buvimas su skirtingais modulio išplėtimo variantais reiškia, kad išoriniai turtingi segmentai yra suskirstyti į daugiklius, o šių daugiklių vidurys bus ryškus. Diyno:

\[\begin(lygiuoti)& \left| x-1 \right|=\left| ((x)^(2))-3x+2 \dešinė|; \\&\left| x-1 \right|=\left| \left(x-1 \right)\left(x-2 \right) \right|. \\pabaiga (lygiuoti)\]

Viena iš modulio galių: $ \left | acdot b \right|=\left| a \right|\cdot \left| b \right|$ (kad modulis būtų labiau panašus į modulių kūrimą), kitu atveju jį galima perrašyti taip:

\[\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|\]

Yak bachimo, turime tinkamą vinic dvigubą daugiklį. Dabar, norėdami pasiimti visus modulius iš vienos pusės, dėl lanko galite kaltinti visą daugiklį:

\[\begin(lygiuoti)& \left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \dešinė|; \\&\left| x-1 \right|-\left| x-1 \right|\cdot \left| x-2 \right|=0; \\&\left| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\pabaiga (lygiuoti)\]

Na, dabar išsiaiškinkime, kas yra pridėjimas prie nulio, jei norime, kad vienas iš daugiklių pasiektų nulį:

\[\left[ \begin(lygiuoti)& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\pabaiga (lygiuoti) \dešinė.\]

Šiame reitinge dviejų modulių lygis buvo iki dviejų paprasčiausių lygių, apie juos buvo kalbama pamokos pradžioje. Tokios lygybės yra tiesiog poroje eilučių.

Danė yra gerbiama, praktiškai galima būti nepaprastai lanksčiam ir nesustabdomam. Tačiau iš tikrųjų galite būti informuoti, kur yra sulankstytos užduotys, sumažinkite jas, kaip galime pagrįstai suprasti. Šiuos modulius taip pat galima derinti su polinomais, aritmetinėmis šaknimis ir logaritmais. Ir tokiose situacijose galima sumažinti ugnies persmelktą kaltės dėl kažko pančių kelią, jo gali atsirasti vis daugiau nei upė.

Dabar norėčiau nupiešti dar vieną lygų, lyg iš pirmo žvilgsnio galėčiau atrodyti miglota. Ant naujų "lipnių" turtingų besimokančiųjų, navit te, jakų vvazhayut, sho gerai sutvarkyti moduliuose.

Prote tse rіvnyannya vіrishuєtsya navіt paprastesnis, nuleiskite tuos, kuriuos pažvelgėme anksčiau. Kai tik ką nors suprasite, imkitės dar vienos gudrybės, kad puikiai suderintumėte modulius.

Otzhe, Rivnyanya:

\[\left| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\]

Hі, tse ne drukarska, atsiprašau: patys mizh moduliai yra pliusas. Ir mes turime žinoti, kad tokiam $x$ dviejų modulių suma yra lygi nuliui. :)

Kas turi problemų? Ir problema ta, kad odos modulis yra teigiamas skaičius, bet kraštutiniu atveju jis yra nulis. Kaip sudėjus du teigiamus skaičius? Akivaizdu, kad dar kartą peržiūriu teigiamą skaičių:

\[\begin(lygiuoti)& 5+7=12 \gt 0; \& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(lygiuoti)\]

Likusią eilutės dalį galima įsivaizduoti: vienas lašas, jei modulių suma lygi nuliui, tai odos modulis lygus nuliui:

\[\left| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\Rodyklė dešinėn \left\( \begin(lygiuoti)& \left| x-((x)^(3)) \right|=0, \\& \left|((x)^(2))+x-2 \right|=0.\\\pabaiga (lygiuoti])

O jei modulis lygus nuliui? Tik viena kryptimi - jei pіdmodulny vіraz dorіvnyuє nulis:

'

Tokia tvarka turime tris taškus, kuriuose pirmasis modulis atstatomas į nulį: 0, 1 ir −1; o taip pat du taškai, kuriuose kitam moduliui nustatomas nulis: −2 ir 1. Tačiau mums būtina, kad moduliai vienu metu būtų nustatyti į nulį, todėl tarp žinomų skaičių reikia pasirinkti t, kuris apima iki abiejų aibių. Akivaizdu, kad tokių skaičių yra daugiau nei vienas: $x=1$ — tai bus likutinė vertė.

padalijimo būdas

Na, mes jau pažiūrėjome į porą išvakarėse ir suplanavome beasmenius priėmimus. kodel tu viska galvoji? Ir ašis i ni! Iš karto galime pažvelgti į galutinį priėmimą – ir tuo pačiu svarbiausią. Atkreipkite dėmesį į rivnyan іz modulio padalijimą. Apie ką tu kalbi? Atsisukime šiek tiek atgal ir atrodykime kaip paprastas lygus. Pavyzdžiui, tse:

\[\left| 3x-5\right|=5-3x\]

Iš esmės mes jau žinome, kaip taip elgtis, nes standartinė formos $\left| konstrukcija f\left(x \right) \right|=g\left(x \right)$. Ale pabandyk stebėtis trocho kokybe po kitu gaubtu. Tiksliau pažiūrėkime į virazą, ką stovėti po modulio ženklu. Spėju, kad bet kurio skaičiaus modulis gali būti lygus pačiam skaičiui arba gali būti priešingas šiam skaičiui:

\[\left| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end (lygiuoti) \right.\]

Vlasne, šis neaiškumas turi visą problemą: keičiasi submodulių skaičius (verta keisti), mums neaišku, ar tai teigiama, ar neigiama.

Bet kas, jei, kita vertus, vimagati, kad skaičius būtų teigiamas? Pavyzdžiui, tarkime $3x-5 \gt 0$ – kokiu būdu garantuotai paimsime teigiamą skaičių po modulio ženklu, o kurį patį modulį galima iškviesti dar kartą:

Esant tokiam rangui, mūsų uolumas apsimesti tiesine linija, nes lengva prisiekti:

Tiesa, viskas, ką apie tai galvojate, gali būti protinga tik protui $3x-5 \gt 0$ – mes patys supažindinome su geriausiais, kad modulį būtų galima vienareikšmiškai atrakinti. Taigi įdėkime žinias apie $x=\frac(5)(3)$ į mintis ir pakartokime:

Norėdami išeiti, mūsų pagalba nelaimi priskirtos $x$ vertės, nes Viraz atrodė lygus nuliui, bet mums reikia, kad jis būtų griežtai didesnis už nulį. Žurbinka. :(

Ale nieko didelio! Kitas variantas $3x-5 \lt 0$. Dar daugiau: dar vienas taškas $3x-5=0$ — reikia taip žiūrėti, kitaip sprendimas bus nesuprantamas. Pažvelkime į $3x-5 \lt 0$ vipadoką:

Akivaizdu, kad modulis pažymėtas minuso ženklu. Bet vėlgi situacija yra nuostabi: aš kairiarankis ir tuo pačiu dešiniarankis tas pats virazas:

Tsikavo, su tokiais $x$ 5-3x$ bus brangiau nei 5-3x$? Tokių lygių akivaizdoje Kapitonas akivaizdus, ​​užspringęs kulnu, bet žinome: ceremonija tam lygi, tobto. vono vіrne kad ir kokia būtų pakeitimo prasmė!

O tse reiškia, kad mus valdo $x$. Vodnocha mes turime є obmezhennya:

Kitaip tariant, tai bus ne trumpas skaičius, o visas intervalas:

Nareshti prarado dar vieną perspektyvą: $3x-5=0$. Čia viskas paprasta: modulis bus lygus nuliui, o nulio modulis bus lygus nuliui (jis nėra tiesiogiai tariamas):

Ale todі vhіdne rіvnyannya $ \ left | 3x-5 \right|=5-3x$ perrašykite taip:

Mes jau atėmėme šaknį daugiau, jei pažiūrėtume į $3x-5\gt 0$ kritimą. Negana to, šaknies kaina už sprendimus lygi $3x-5=0$ – keitimo vertė, kaip mes patys įvedėme, norint iš naujo nustatyti modulį.

Šia tvarka krimto intervalas yra mums dominuojantis skaičius, esantis pačioje intervalo pabaigoje:

Liekamoji konsistencija: $x\in \left(-\infty ;\frac(5)(3) \right]$ Nelabai garsu daryti tokius mėšlungius vіdpovіdі iki paprasto (iš esmės – linijinio) suderinimo su moduliu. dpovіdі tokiose nelygybėse gali pasirodyti visiškai neproducuojama.

Kur dar svarbiau: mes kruopščiai sukūrėme universalų algoritmą, kaip išspręsti problemą su moduliu! І visas algoritmas sudaromas iš sekančių žingsnių:

1. Prilyginkite odos modulį, kuris yra lygus, nuliui. Atimame šprotus vienodai;
2. Sudėkite visus skaičius vienodus ir skaičių eilutėje įdėkite šaknį. Dėl to yra tiesioginis intervalų padidėjimas, ant odos visi moduliai yra vienareikšmiškai išvystyti;
3. Virishiti vihіdne іvnyannja odos intervalui ir ob'єdnati otrimaniі vіdpovіdі.

Nuo aš visų! Liko mažiau nei vienas maistas: kur turėtų eiti šaknys, nupjautos ant 1 nėrimo? Tarkime, kad turime dvi šaknis: $ x = 1 $ i $ x = 5 $. Smarvė skaičiais kilo tiesiai 3 vienetams:

Na, kokie čia intervalai? Supratau, kad jų yra trys:

1. Naylivishy: $x \lt 1$ — pats vienas elementas neįtrauktas į intervalą;
2. Centrinis: $1\le x \lt 5$ - ašis čia yra viena intervale įvesti, prote neįvesti penki;
3. Tinkamas: $x\ge 5$ – Penkios dienos čia!

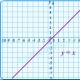
Manau, jūs jau supratote įstatymą. Odinis intervalas apima kairįjį galą ir neapima dešiniojo.

Iš pirmo žvilgsnio toks įrašas gali pasirodyti netvarkingas, nelogiškas ir miglotas. Ale posūkis: šiek tiek pasimokę pamatysite, kad pats toks pidkhidas yra pats pranašiausias ir, dėl to, modulių vienareikšmiškai nekursite. Geriau laimėti tokią schemą, tada pagalvokite apie tai: pasukite į kairę / į dešinę dabartiniu intervalu arba meskite jogą į puolimą.

Kuri pamoka baigsis. Priimk savarankiško aprūpinimo užduotį, treniruokis, varžykis su įtakomis – ir dirbsime ateinančioje pamokoje, kuri bus skirta modulių nervingumui.

Vaizdo funkcija y=|x|.
Funkcijos y = -x grafikas.

Pažvelkime į paprasčiausią būdą – funkciją y=|x|. Modulio tikslais galima:

Taigi, jei x≥0, funkcija y=|x| zbіgaєtsya su funkcija y \u003d x, a x x | (1 pav.).

Nesunku pastebėti, kad šis grafikas yra maždaug ta pati funkcijos y = x grafiko dalis, todėl ji yra ne žemiau už ašį OX ir tiesę, kuri paimta iš ašies OX veidrodinių vaizdų, trečioji dalis, kad ji yra žemiau linijos ašies OX.
Šis metodas yra atsitiktinis funkcijos y=|kx+b| grafiko raginimui.
Nors funkcijos y=kx+b grafikas parodytas 2 paveiksle, funkcijos y=|kx+b| є linija, parodyta 3 pav.

Užpakalis 1. Indukuokite funkcijos y=||1-x 2 |-3| grafiką.
Iškvieskime funkcijos y=1-x 2 grafiką ir atliksime operaciją „modulis“ (grafo dalis, nubrėžta žemiau OX ašies, simetriškai perkeliama išilgai OX ašies).

Vikonaemo zsuv grafika sumažėjo 3.

Mums reikia operacijos „modulis“ ir atimti funkcijos y=||1-x 2 |-3| likutinį grafiką.

užpakalis 2. Indukuokite funkcijos y=||x2-2x|-3| grafiką.
Dėl transformacijos gauname y=|x2-2x|=|(x-1)2-1|. Padarykime funkcijos y = (x-1) 2 -1 grafiką: padarykime parabolę y = x 2 ir pasukime dešine per 1 ir žemyn 1.

Būtina atlikti naują operacijos „modulį“ (grafo dalis, išplėsta žemiau OX ašies, simetriškai perkeliama išilgai OX ašies).

Sumažiname grafiką 3 ir atliekame „modulio“ operaciją, todėl pašaliname likusį tvarkaraštį.

3 pavyzdys. Sukurkite funkcijos tvarkaraštį.
Norėdami atidaryti modulį, turite peržiūrėti du rodinius:
1)x>0, tada modulis bus atidarytas su ženklu "+" =
2) x =

Sudaryk pirmojo susitikimo grafiką.

Vidkinemo grafikos dalis, de x

Turėkime kito rodinio grafiką ir panašiai kaip toje dalyje, kur x>0, rezultatas atimamas.

Paimkime du grafikus ir paimkime likusį.

4 pavyzdys. Sukurkite funkcijos tvarkaraštį.
Pradėkime nuo funkcijos tvarkaraščio. Kam nesunku matyti visą dalį, atimkite. Už stalo yra vertė, mes priimame tvarkaraštį.

Būtina atlikti modulio operaciją (grafo dalis, išskleista žemiau OX ašies, simetriškai atvaizduojama išilgai OX ašies). Mes priimame likusį tvarkaraštį

5 pavyzdys. Indukuokite funkcijos y=|-x2+6x-8| grafiką. Pradėkime nuo paprastos funkcijos iki y=1-(x-3) 2 ir mums reikės tvarkaraščio

Dabar galime atlikti „modulio“ operaciją ir matyti dalį grafiko po ašimi OX ir išilgai ašies OX

6 pavyzdys. Indukuokite funkcijos y=-x2+6|x|-8 grafiką. Be to, galime lengvai veikti iki y=1-(x-3) 2 ir mums reikės tvarkaraščio

Dabar galime atlikti „modulio“ operaciją ir, matyt, grafiko dalis yra oY ašies dešinėje, kairėje

7 pavyzdys. Sukurkite funkcijų tvarkaraštį . Leiskite mums suplanuoti funkciją

Leiskite mums suplanuoti funkciją

Atrodo, kad lygiagretus perkėlimas į 3 pavienius vyniotuvus dešinėje ir 2 įkalnėje. Ateityje pamatysiu tvarkaraštį:

Galime atlikti „modulio“ operaciją ir įsivaizduoti grafiko dalį į dešinę nuo tiesės x=3 kairėje pusplokštumoje.

Modulio ženklas, ko gero, yra vienas žinomiausių matematikos reiškinių. Tuo zv'yazku z tsim pas turtingus moksleivius po mitybos, kaip buduvat funkcijų tvarkaraščius, scho atkeršyti už modulį. Praneškime apie maisto grandinę.

1. Pobudova grafinės funkcijos, kuo pakeisti modulį

1 pavyzdys.

Indukuokite funkcijos y = x 2 - 8 | grafiką x | + 12.

Sprendimas.

Funkcijos paritetas yra reikšmingas. Y(-x) reikšmės yra paimtos iš y(x) reikšmių, todėl funkcija yra suporuota. Todi її tvarkaraštis simetriškas shdo osі Oy. Tai bus funkcijos y = x 2 - 8x + 12 grafikas, kai x ≥ 0, o Oy grafikas bus rodomas simetriškai neigiamam x (1 pav.).

užpakalis 2.

Būsimas tvarkaraštis mintis y = | x 2 - 8x + 12 |.

– Kokia yra siūlomos funkcijos apimtis? (y ≥ 0).

– Kaip perbraižytas grafikas? (Virš abscisės viršaus arba išsikišęs її).

Tse reiškia, kad funkcijos grafikas yra tokia tvarka: funkcijos y \u003d x 2 - 8x + 12 grafikas užpildys grafiko dalį, esančią virš linijos Ox, nesikeičiant, o grafiko dalis, esanti po abscisių linija, simetriškai rodo, kad ašiai Ox (2 pav.).

3 pavyzdys.

Norėdami paskatinti funkcijos y = | grafiką x 2 - 8 | x | + 12 | atlikti transformacijų derinį:

y = x 2 - 8x + 12 → y = x 2 - 8 | + 12 → y = | x 2 - 8 | x | + 12 |.

Pasiūlymas: 3 pav.

Pažvelkite į sąžiningos funkcijų transformaciją į visas funkcijas. Padarykime lentelę:

2. Pobudovos funkcijų grafikai, kaip formulėje "įterpti modulius"

Jau sužinojome apie kvadratinės funkcijos užpakalis, kaip atkeršyti modulį, taip pat apie pagrindines y = f (| x |), y = | formos funkcijų grafikų kūrimo taisykles. f(x) | ir y = |f(|x|)|. Qi transformacija padės mums valandą pažvelgti į įžeidžiantį užpakaliuką.

4 pavyzdys.

Pažiūrėkime į funkciją, kurios tipas y = |2 – |1 – |x|||. Viraz, kuris nustato funkciją, pašalinkite modulio įterpimą.

Sprendimas.

Pagreitinimas geometrinių transformacijų metodu.

Užsirašykime paskutinių pakeitimų ir zrobimo žibintus fotelio viduryje (4 pav.):

y=x → y=| x | → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1 | + 2 → y = | 2 - | 1 - | x | | |.

Pažiūrėkime į vipadki, jei simetrijos transformacija ir lygiagretus perkėlimas yra pagrindinė tvarkaraščių skatinimo technika.

5 pavyzdys.

Sukelkite funkcijos grafiką į formą y \u003d (x 2 - 4) / √ (x + 2) 2.

Sprendimas.

Pirmą kartą bus tvarkaraštis, perdarysime formulę, kuri yra duota funkcija, kuri atimama, kitu atveju funkcijos analitinė užduotis (5 pav.).

y = (x 2 - 4) / √ (x + 2) 2 = (x - 2) (x + 2) / | x + 2 |.

Rozkriёmo prie modulio reklamjuostės:

Jei x > -2, y = x - 2 ir x< -2, y = -(x – 2).

Paskirties sritis D(y) = (-∞; -2)ᴗ(-2; +∞).

Reikšmės sritis E(y) = (-4; +∞).

Taškai, kuriuose grafikas keičiasi išilgai koordinačių ašių: (0; -2) ir (2; 0).

Funkcija keičiasi per visus x intervalus (-∞; -2), auga iš x iš -2 iki +∞.

Čia turėjome galimybę iššifruoti modulio ženklą ir odos bėrimo funkcijos grafiką.

6 pavyzdys.

Pažiūrėkime į funkciją y = | x + 1 | - | x - 2 |.

Sprendimas.

Tyrinėjant modulio ženklą, būtina pažvelgti į skirtingus submodulio eilėraščių ženklų derinius.

Galbūt šiek tiek vipadki:

(x + 1 - x + 2 = 3, kai x ≥ -1 ir x ≥ 2;

(-x - 1 + x - 2 = -3, su x< -1 и x < 2;

(x + 1 + x - 2 = 2x - 1, jei x ≥ -1 i x< 2;

(-x - 1 - x + 2 = -2x + 1, su x< -1 и x ≥ 2 – пустое множество.

Ta pati išvaizdos funkcija matime look:

(3, jei x ≥ 2;

y = (-3, ties x< -1;

(2x – 1, kai -1 ≤ x< 2.

Mes pašalinome vienkartinio rinkinio funkciją, kurios grafikas pavaizduotas kaip mažas 6.

3. Funkcijų grafikų formavimo indukavimo algoritmas

y = a 1 | x - x 1 | + a 2 | x - x 2 | + … + a n | x - x n | + kirvis + b.

Prie priekinio užpakalio lengva atidaryti modulio ženklus. Jei modulių suma didesnė, tai problematiška žiūrėti į visas submodulių ženklų kombinacijas. Kaip galėčiau kam suplanuoti funkcijos tvarkaraštį?

Svarbu, kad grafas turi lamaną su viršūnėmis taškuose, kad abscisės gali būti -1 ir 2. Esant x = -1 ir x = 2 submoduliai lygūs nuliui. Praktiškai priartėjome prie taisyklės skatinti tokius tvarkaraščius:

Funkcijos grafikas forma y = a 1 | x - x 1 | + a 2 | x - x 2 | + … + a n | x - x n | + kirvis + b є laman su neišsenkamais ekstremaliais lankais. Norint sukelti tokį lamaną, pakanka žinoti visas її viršūnes (viršūnių abscisis є nulis pіdmodulnyh virazіv) ir vieną valdymo tašką kairėje ir dešinėje nenuluptų lankų.

Vadovas.

Indukuokite funkcijos y = | grafiką x | + | x - 1 | + | x + 1 | o žinoti yra mažiausiai svarbu.

Sprendimas:

Nulis submodulinių virusų: 0; -1; 1. Lamanoi viršūnės (0; 2); (-13); (13). Kontrolinis taškas dešiniarankis (2; 6), blogis (-2; 6). Bus tvarkaraštis (7 pav.). min f(x) = 2.

Pritrūko maisto? Nežinote, kaip suplanuoti funkciją su moduliu?
Aš padėsiu jums padėti mokytojui -.

blog.website, su nauja arba privačia medžiagos kopija, atsiųsta ant originalaus įrišimo.